こんにちは。
よく、平均年収という言葉を耳にしますよね。2017年の平均年収は、国税庁の民間給与実態統計調査によると、下表の通りです。
| 平均年収 | 合計 | 正規社員 | 非正規社員 |
| 男性 | 531.5万 | 547.5万 | 229.4万 |
| 女性 | 287.0万 | 376.6万 | 150.8万 |
| 合計 | 432.2万 | 493.7万 | 175.1万 |
さて、みなさんこの数値を見て、自分より高いと感じるか、低いと感じるか、どちらでしょうか。恐らく、自分より高いと感じる人の方が多いのではないでしょうか。値の集合の真ん中を特徴付ける値は「平均値」だけではなく「中央値」というものがあります。
この記事では、平均年収を例として、平均値と中央値の違いを説明していきます。
平均値とは
では、ここでいう平均年収を表す「平均値」とはどういうものなのでしょうか。そんなの知ってるよ!という方も多いかと思いますが、そういった方は読み飛ばしてください。
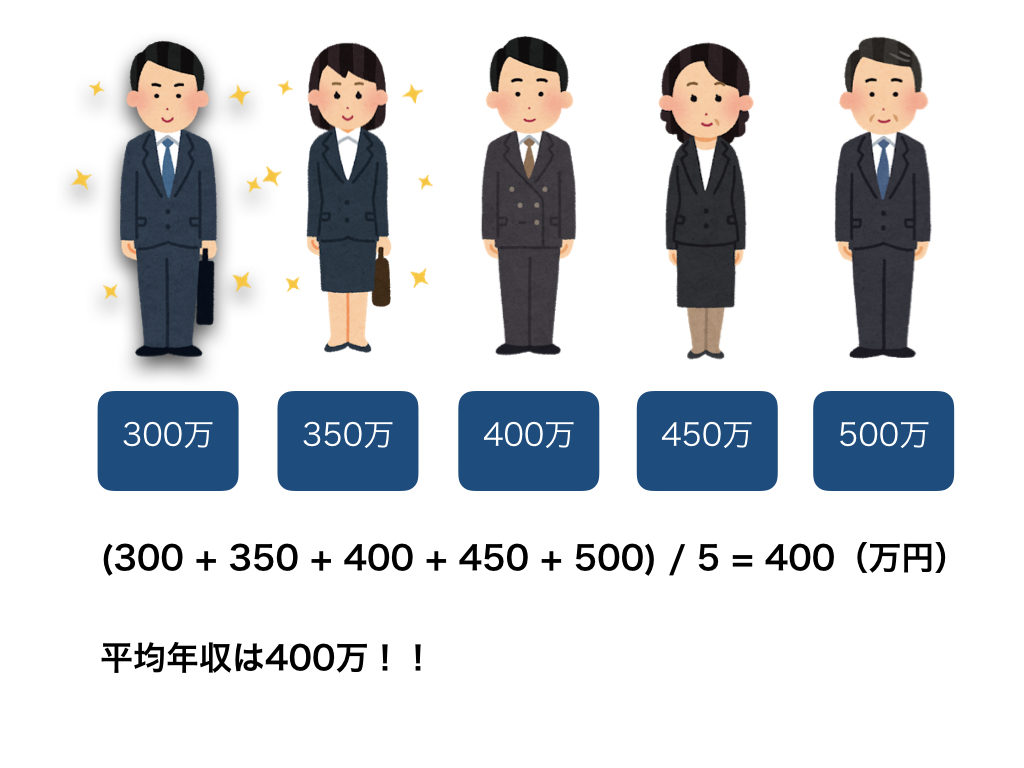
例えば、年収がそれぞれ300万、350万、400万、450万、500万の人がいると仮定します。
その時、平均年収は下図のとおり400万円になります。
それでは、以下のように、300万、400万、500万、600万、1500万の人がいる場合はどうでしょう。
あら不思議!平均年収は660万になります。
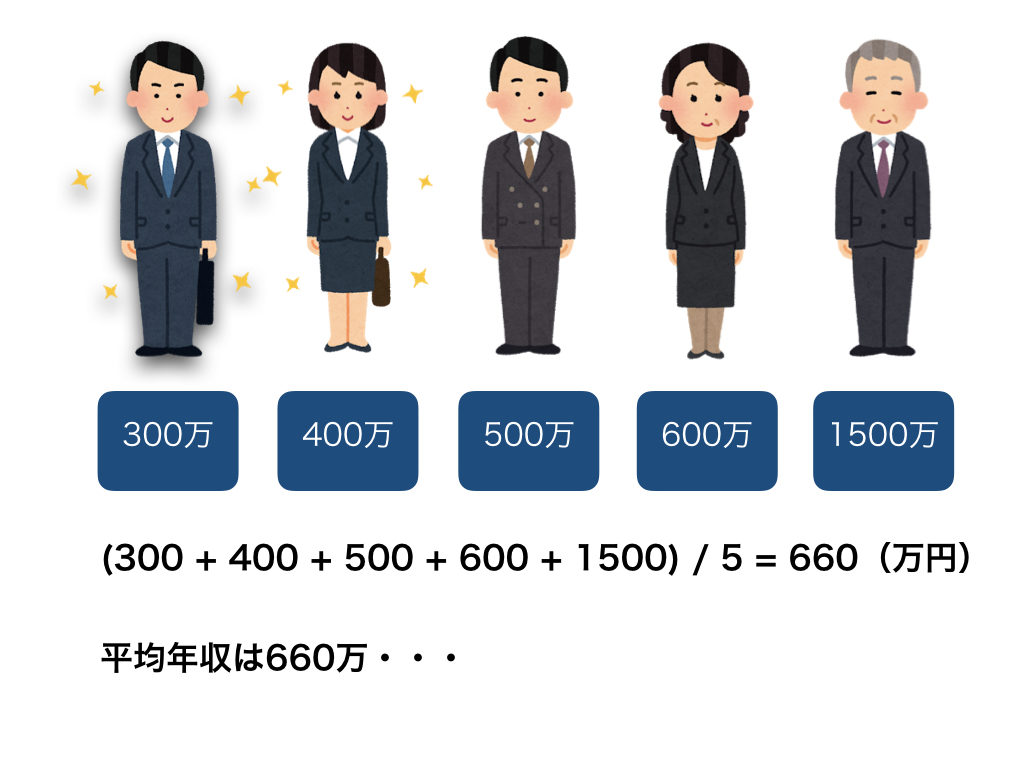
見ての通り、平均値は660万ですが、それを上回る人は一人しかいませんね。年収が平均より低い人が過半数だとしても、この例のように年収が高い人がいると平均値を大きく上げてしまうことがある、ということです。このように、他の値と比べて大きく外れた値がある場合、平均値は影響を受けてしまいます。
中央値とは
それでは、上記を中央値で見た場合はどうなるのでしょうか。まずは一つ目の、年収がそれぞれ300万、350万、400万、450万、500万の人がいる場合です。
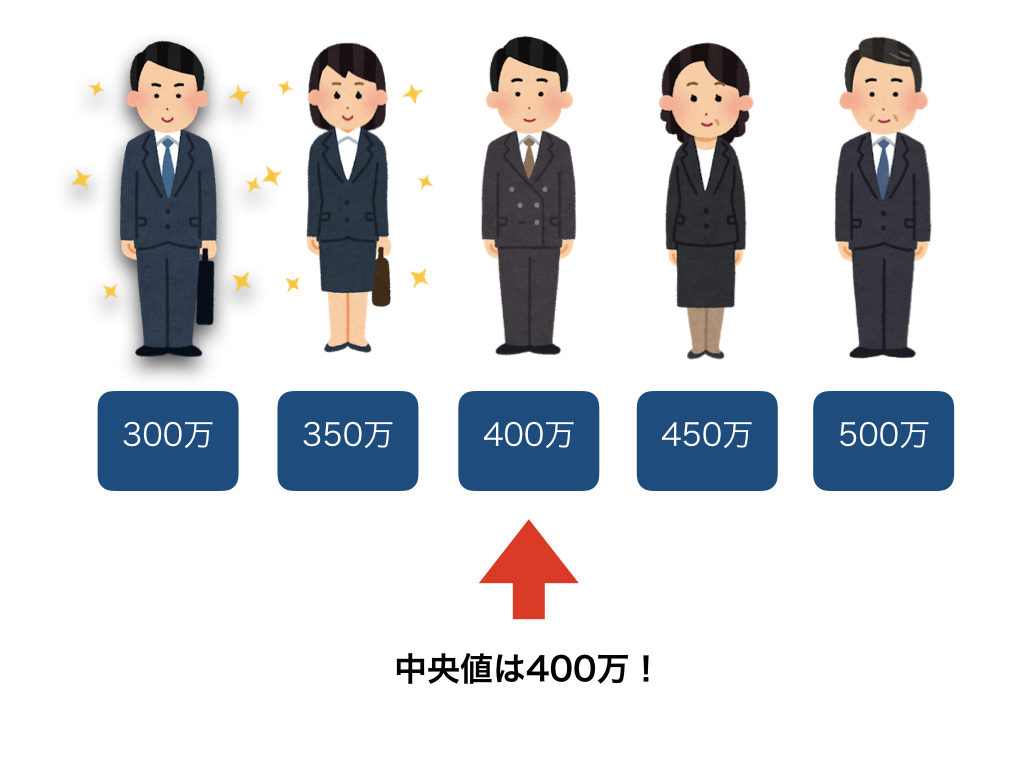
このように、値の分布が均等の場合は平均値と変わりありませんね。
それでは、300万、400万、500万、600万、1500万の人がいる場合はどうでしょうか。
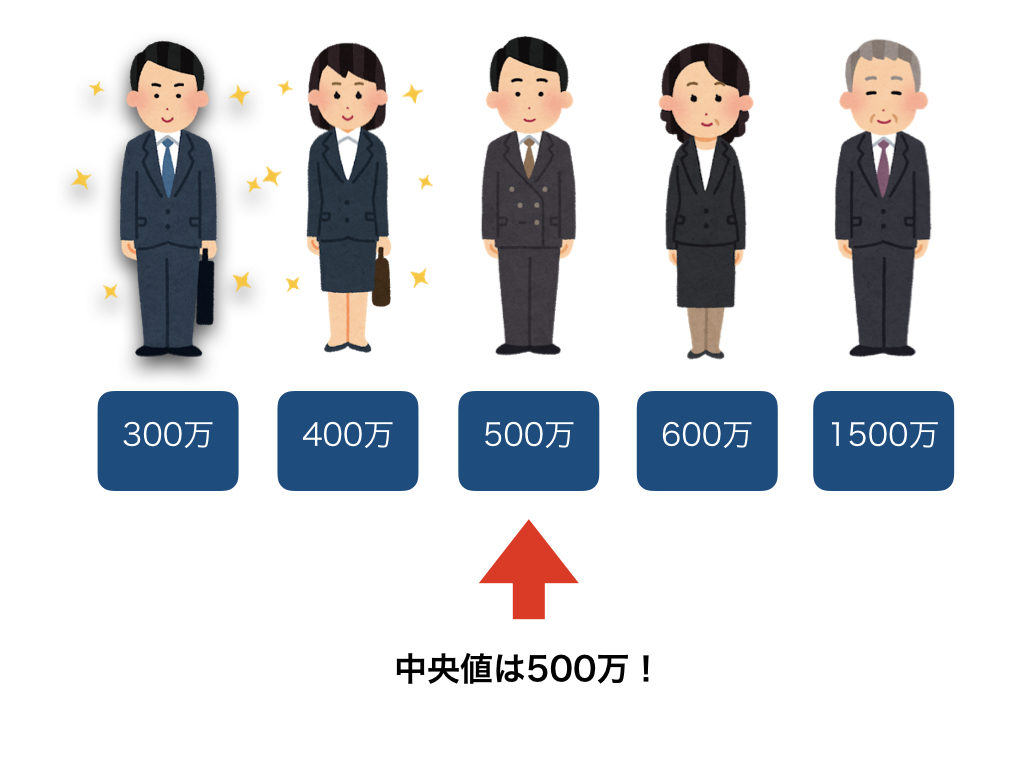
1500万の人がいても、中央値は500万です。平均値で算出した660万に比べると、実態に沿った集合の中心といった感じがしますよね。このように、他の値と比べて大きく外れた値がある場合でも、その影響を受けづらいのが中央値の特徴です。
平均値と中央値の向き不向き
平均値のメリットは、算出のために全ての値を利用するため、「全て値を代表した値」として使うことができる点です。しかしながら、上述の例のように、他の値と比べて大きく外れた値があった時にはその影響を大きく受けてしまうというデメリットがあります。
中央値のメリットは、他の値と比べて大きく外れた値の影響を受けずに値の集合の中心を算出することができる点です。しかしながら、順番に数えて真ん中の値しか利用しないので、値の集合の変化や傾向を観察するには不向きであるというデメリットがあります。
2017年の中央値はどれくらいか?
それでは、冒頭に2017年の平均年収の表を載せましたが、これを中央値で見るとどれくらいなのでしょうか。国税庁の民間給与実態統計調査に中央値は掲載されていませんので正確な値はわかりませんが、おおよその値を算出してみました。100万円単位で人数が掲載されているので、100万円の幅の中では均等に分布しているとして試算しています。
| 平均年収(再掲) | 合計 | 正規社員 | 非正規社員 |
| 男性 | 531.5万 | 547.5万 | 229.4万 |
| 女性 | 287.0万 | 376.6万 | 150.8万 |
| 合計 | 432.2万 | 493.7万 | 175.1万 |
| 年収中央値(推定) | 合計 | 正規社員 | 非正規社員 |
| 男性 | 460万 | 485万 | 200万 |
| 女性 | 300万 | 350万 | 140万 |
| 合計 | 370万 | 440万 | 155万 |
こうして並べてみると、中央値は女性の合計以外は平均値より低いことがわかりますね。女性の場合、正規労働者の人数が大体1000万人に対して非正規労働者が800万人と比較的多いため、全体の平均値が低めに出ているためですね。それ以外の値、特に男性の合計や正規社員は、中央値より平均値の方が1割以上低いですね。これが、平均年収を耳にしたときにそれより低いと感じる人が多い正体ですね。
まとめ
今回は、平均値と中央値の違いを年収を例にしてまとめました。
ニュースなどで平均年収は〜という記事を見たときには、こういうことなんだということを頭の片隅に入れておくと、より理解しやすいのではないかと思います。自身の年収がどの程度なのかを把握する上でも、参考にしていただければと思います。